[2021.01.06] 모각코 2회 - Brute-Force
1. 학습 목표
- 큐와 스택에 대해 알아보고 백준 문제 풀기 + DP 2문제 풀이
2. 후기
- 백준 9012, 10799 둘 다 2학기 중에는 풀기를 시도하다가 포기한 문제였다.
이번 기회에 스택에 대해 이해하고 차근하게 문제에 접근하면서 풀어낼 수 있었다.
dp문제도 4개를 풀이하지 못해 쌓아두고 있었는데, 2문제를 풀어낼 수 있었다.
못 풀겠다고 포기했던 문제들을 다시 도전하면서 실패할 때도 있지만 성공하는 경우에는 성취감이 컸다.
기존에 도전하려고 했던 C++ 알고리즘 책은 JAVA로 좀 더 모든 알고리즘에 익숙해진 후에 도전하기로 결정했다.
3. 학습 내용
- Stack(스택)
'쌓다'라는 의미를 가진 스택은 LIFO(Last In First Out)의 특징을 가지고 있다.
이에 관련된 자바 메서드로는 크게 5가지가 있다.
Element pop() // 마지막으로 추가된 데이터 삭제
Element push(Element item) // 데이터 추가
Element peek() // 마지막으로 추가된 데이터 조회
Boolean empty() // stack이 비었는지 확인하고 true, false 반환
int search(Object O) // 데이터의 위치 반환
- <백준 9012 JAVA>
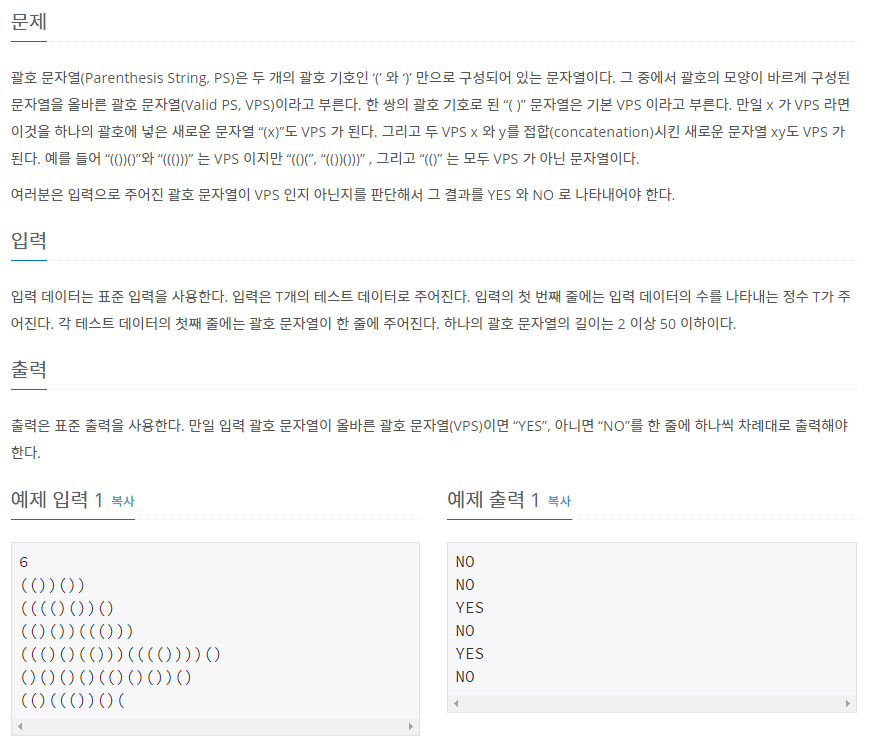
위 주어진 문제에서는 '('와 ')'가 짝이 잘 맞는지 확인하는 문제이다.
각각의 문자열을 배열로 바꿔서 앞에서부터 하나씩 훑으면서
'('의 경우 stack에 넣고 ')'의 경우에는 stack에서 pop을 했다.
다만 위 과정에서 stack이 pop을 해야 하는데 비어있는 경우 바로 false를 반환하도록 했다.
위 과정을 모두 거친 후 stack이 비어있다면 true를 반환하고 아니라면 false를 반환하도록 했다.
import java.io.*;
import java.util.*;
public class N_9012 {
public static boolean test(char[] ch){
Stack<Character> stack = new Stack<>();
for(int k = 0; k<ch.length; k++){
if(ch[k]=='('){
stack.push('(');
}else if(ch[k]==')'){
if(stack.empty()){
return false;
}else{
stack.pop();
}
}
}
if(stack.empty()){
return true;
}else{
return false;
}
}
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader( new InputStreamReader(System.in));
int N = Integer.parseInt(br.readLine());
List<String> answer = new ArrayList<>();
for(int i = 0; i<N; i++){
char[] ch = br.readLine().toCharArray();
if(test(ch)){
answer.add("YES");
}else{
answer.add("NO");
}
}
for(int j = 0; j<answer.size(); j++){
System.out.println(answer.get(j));
}
br.close();
}
}
- <백준 10799 JAVA>

문제를 이해하는 것은 어렵지 않았으나 답을 도출하기 위한 해결법을 떠올리는 것이 시간이 좀 걸렸다.
예제 1)
()(((()())(())()))(())
0 3 3 4 3 3 1
12+5 = 17
예제 2)
(((()(()()))(())()))(()())
3 4 4 5 3 3 1 1
8+9+7 = 24
이렇게 직접 표현하고 나니 풀이법이 눈에 보였다.
()가 있을 경우 stack.size를 더해주며 막대의 시작점인 '('일 때는 stack에 추가해준다.
막대의 종결점인 ')'의 경우에는 () 전의 ')'의 개수를 세고 난 뒤 ()를 만난 후 stack.size를 더해 준 후에 개수만큼 stack.pop을 한다.
이 과정까지 진행을 하고 답을 도출한 결과 예제 1에서는 16, 예제 2에서는 23이 나오면서 마지막 부분의 막대 개수가 반영되지 않는 것을 알게 되었다. 따라서 stack.size를 한 번 더 최종적으로 더해줌으로써 답을 구할 수 있었다.
import java.util.*;
import java.io.*;
public class N_10799 {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader( new InputStreamReader(System.in));
char[] ch = br.readLine().toCharArray();
Stack<Character> stack = new Stack<>();
int result = 0;
int count = 0;
for(int i = 0; i< ch.length; i++){
if(ch[i]=='('){
if(ch[i+1]==')'){
result += stack.size();
for(int k = 0; k<count; k++){
stack.pop();
}
count = 0;
i++;
}else if(ch[i+1]=='('){
stack.add('(');
}
}else if(ch[i]==')'){
count++;
}
}
result += stack.size();
System.out.println(result);
br.close();
}
}
- Dynamic Programming(동적 계획법, 이하 dp)
동적 계획법의 원리는 일반적으로 주어진 문제를 풀기 위해서 문제를 여러 개의 하위 문제로 나누어 푼 다음,
그것을 결합하여 최종적인 목적에 도달하는 것이다.
각 하위 문제의 해결을 계산한 뒤, 그 해결책을 저장하여 후에 같은 하위 문제가 나왔을 경우 그것을 간단하게 해결할 수 있다.
이러한 방법으로 동적 계획법은 계산 횟수를 줄일 수 있다.
특히 이 방법은 하위 문제의 수가 기하급수적으로 증가할 때 유용하다.
(출처_위키백과)
- <백준 2133 JAVA>

이 문제는 점화식을 찾으면 쉽게 풀이할 수 있는 문제이다.
import java.util.*;
import java.math.*;
public class N_2133 {
static int dp[] ;
public static void main(String[] args) {
Scanner scan = new Scanner(System.in);
int n = scan.nextInt();
dp = new int[31];
dp[0] =1;
dp[1] = 0;
if(n>1){
dp[2] = 3;
}
for(int i=4;i<=n;i+=2) {
dp[i] = 3*dp[i-2];
for(int j=0;j<i-2;j+=2) {
dp[i]+=dp[j] * 2;
}
}
System.out.println(dp[n]);
scan.close();
}
}
- <백준 11052 JAVA>

처음 문제를 보았을 때는 도저히 풀이법이 예상 가지 않았다.
dp문제라면 작은것으로부터 큰 결론을 만들어가야 하는데, 어떻게 건드려야 할까 고민하다가
1개의 카드를 가장 비싸게 사는 법인 dp [1]을 시작점으로 놓고,
2개의 카드를 가장 비싸게 사는 법을 1개의 카드를 2개 사는 법과 2개의 카드를 사는 법 중에 비싼 값을 구해 dp [2]로 놓았다.
이후에 dp [n]은 dp [k] + dp [n-k]의 값과 n개의 카드를 사는 법 중 더 비싼 것, 즉 큰 값을 찾아서 dp [n]에 저장했다.
차근차근 1개를 가장 비싸게 사는 법에서 시작해서 n개를 가장 비싸게 사는 법에 도달하는 것이다.
import java.io.*;
public class N_11052 {
public static int[] dp = new int[1001];
public static int count(int N){
int max = 0;
for(int k = 1; k<N; k++){
int result = dp[k]+dp[N-k];
max = Math.max(result, max);
}
return max;
}
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader( new InputStreamReader(System.in));
int N = Integer.parseInt(br.readLine());
String[] s = br.readLine().split(" ");
int[] arr = new int[N+1];
arr[0] = 0;
for(int i = 0; i<s.length; i++){
arr[i+1] = Integer.parseInt(s[i]);
}
dp[1] = arr[1];
for(int i = 2; i<=N; i++){
dp[i] = Math.max(arr[i], count(i));
}
System.out.println(dp[N]);
br.close();
}
}